Calcolare l’altezza di un triangolo isoscele è una procedura matematica fondamentale e utile, che trova applicazione in vari contesti geometrici e scientifici. I triangoli isosceli, caratterizzati da due lati congruenti e due angoli congruenti, offrono interessanti sfide e soluzioni per determinare la lunghezza dell’altezza, ossia la distanza verticale tra la base e il vertice.
In questo articolo, esploreremo diverse formule e metodi che consentono di calcolare l’altezza di un triangolo isoscele. Ti guideremo attraverso le procedure passo dopo passo, illustrando come applicare queste formule in situazioni pratiche. Imparerai non solo a determinare l’altezza di un triangolo isoscele in base alle informazioni a tua disposizione, ma anche a comprendere la logica matematica che sta dietro a questi calcoli.
Che tu sia uno studente che desidera approfondire le sue competenze matematiche o una persona interessata alla geometria, questo articolo ti fornirà le conoscenze necessarie per affrontare con successo questo tipo di calcolo geometrico.
Indice Guida Gratis:
Comprendere il Triangolo Isoscele
Prima di iniziare a calcolare l’altezza, è importante comprendere le caratteristiche di un triangolo isoscele. Le principali proprietà di questo tipo di triangolo includono:
- Due lati congruenti: I due lati che si oppongono agli angoli congruenti sono della stessa lunghezza.
- Due angoli congruenti: Gli angoli formati dalla base del triangolo con gli altri due lati sono della stessa misura.
Trovare e calcolare altezza Triangolo Isoscele
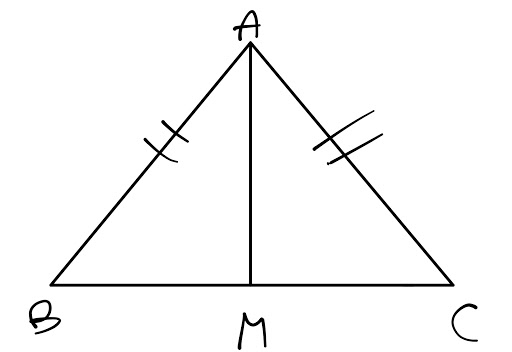
Nel caso in cui si volesse risalire all’altezza di un triangolo isoscele è necessario ricordare che il lato che tra i tre è disuguale divide il triangolo in due triangoli rettangoli identici (nel guardare la figura lo si capisce in modo immediato, ma in questo contesto ci si deve accontentare di una spiegazione verbale).
I due triangoli rettangoli sono simmetrici ed hanno come ipotenusa uno dei due lati uguali e come cateti rispettivamente l’altezza che si intende cercare e la metà del lato disuguale. Per calcolare l’altezza basta calcolare la radice quadrata dell’ipotenusa dei due triangoli rettangoli al quadrato a cui va sottratto il valore della metà del lato disuguale al quadrato.
Più difficile da dirsi a parole che da farsi. Si tratta di una formula fissa alla quale si arriva con un minimo di logica e mettendo a frutto le conoscenze di base in geometria. Nei libri di scuola vengono spesso proposti problemi nei quali presentati dei terreni con la forma di un triangolo isoscele o semplicemente, in modo chiaro, veniva chiesto di calcolare l’altezza partendo dai lati. Questo se si ha a disposizione la misura dei lati.
Calcolo dell’Altezza con una Base e un Lato
Uno dei modi più comuni per calcolare l’altezza di un triangolo isoscele è quando conosci la lunghezza della base (b) e uno dei lati congruenti (a). Ecco la formula:
Dove:
- h rappresenta l’altezza del triangolo isoscele.
- a è la lunghezza di uno dei lati congruenti.
- b è la lunghezza della base.
Ecco come puoi utilizzare questa formula:
- Conosci i valori di a e b del tuo triangolo isoscele.
- Sostituisci questi valori nella formula e calcola l’altezza h.
Dall’area all’altezza del triangolo isoscele
Se invece si dispone dell’area del triangolo allora l’altezza sarà data dall’area divisa la base (o meglio, area diviso lato disuguale) ed a ciò si arriva ragionando attorno alla formula dell’area di un triangolo (base x altezza diviso due).
Ovviamente le formule su indicate sono valide per tutti i triangoli isosceli, di qualunque tipo essi siano, visto che hanno tutti le stesse caratteristiche e le loro misure si calcolano allo stesso modo.






