I logaritmi sono un concetto matematico affascinante e potente che si trova al cuore di molte discipline scientifiche e ingegneristiche. Se stai iniziando a studiare i logaritmi o sei semplicemente curioso di sapere cosa siano e perché dovresti dedicare del tempo a comprenderli, sei nel posto giusto.
In questo articolo, esploreremo il mondo dei logaritmi, spiegando cosa sono in modo chiaro e semplice. Inoltre, scopriremo le numerose applicazioni pratiche dei logaritmi in vari campi, dalle scienze esatte all’economia, dall’ingegneria alla biologia.
Imparerai anche perché lo studio dei logaritmi è fondamentale per costruire una solida base matematica che ti consentirà di affrontare complessità crescenti in molte discipline accademiche e professionali. Quindi, preparati a immergerti nel mondo affascinante dei logaritmi e a scoprire perché meritano la tua attenzione e il tuo impegno nello studio.
In matematica, il logaritmo è un operatore, o meglio una funzione, che indica l’esponente da assegnare ad un data base per ottenere l’argomento del logaritmo.
Ad esempio, il logaritmo in base 2 di 8 è 3, perché 2 elevato a 3 è proprio uguale all’argomento del logaritmo, cioè 8.
I logaritmi più comunemente usati sono i logaritmi in base 10, quelli in base 2 e quelli in base e, cioè il cosiddetto numero di Nepero il cui valore è circa 2.71828.
Indice Guida Gratis:
Quando sono nati i Logaritmi
I logaritmi sono una scoperta matematica fondamentale attribuita a John Napier, un matematico scozzese del XVI secolo. Napier introdusse per la prima volta i logaritmi nei suoi lavori pubblicati nel 1614 e nel 1619. La sua opera principale, intitolata “Mirifici Logarithmorum Canonis Descriptio” (Descrizione dei meravigliosi canoni dei logaritmi), presentava una tabella di logaritmi di numeri da 1 a 1000.
L’idea di base di Napier era semplificare i calcoli complessi, in particolare quelli legati alla moltiplicazione e alla divisione, trasformandoli in operazioni più semplici di addizione e sottrazione. Questo si è rivelato di grande utilità in campi come l’astronomia, la navigazione e la scienza, dove calcoli elaborati erano essenziali.
I logaritmi hanno avuto un impatto rivoluzionario sulla pratica scientifica e matematica dell’epoca, accelerando notevolmente la precisione e l’efficienza dei calcoli. L’opera di Napier ha aperto la strada a ulteriori sviluppi nel campo dei logaritmi da parte di matematici successivi, come Henry Briggs, che ha introdotto il sistema logaritmico comune che utilizziamo ancora oggi.
Logaritmi: cosa sono
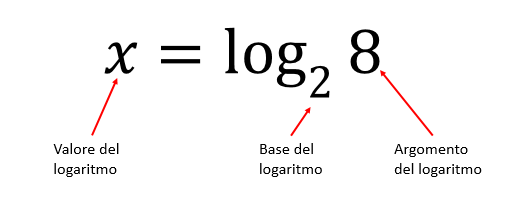
Una scala logaritmica (o scala logaritmica) è un modo per visualizzare i dati numerici su un intervallo molto ampio di valori in modo compatto: in genere i numeri più grandi nei dati sono centinaia o addirittura migliaia di volte più grandi dei numeri più piccoli.
Il logaritmo, in una delle basi sopra citate o nella generica base a, è visto anche come funzione, ovvero come la funzione che associa alla variabile contenuta nell’argomento del logaritmo, l’esponente da assegnare alla base per ottenere la variabile stessa.
Pertanto, la funzione logaritmo è l’inversa della funzione esponenziale. Il dominio della funzione logaritmo è l’asse dei numeri reali positivi, eccetto lo zero: ciò significa che la variabile x, argomento del logaritmo, non può essere negativa, né nulla. Al contrario, il condominio, ovvero l’insieme dei valori che può assumere la funzione, copre tutto l’insieme dei numeri reali, sia positivi che negativi.
A cosa servono i Logaritmi

In matematica, i logaritmi sono molto usati perché godono di alcune proprietà fondamentali, che valgono qualunque sia la base, tra le quali troviamo le seguenti: il logaritmo di un prodotto è uguale alla somma dei logaritmi dei due fattori (ad esempio il logaritmo di 20 è uguale al logaritmo di 5 sommato al logaritmo di 4).
Il logaritmo di un rapporto è uguale alla differenza dei logaritmi del numeratore e del denominatore (ad esempio il logaritmo di 5 è uguale al logaritmo di 10 meno il logaritmo di 2); il logaritmo di un numero elevato ad n è uguale a n moltiplicato per il logaritmo del numero (ad esempio il logaritmo di 8 è uguale a 3 volte il logaritmo di 2). L’utilità pratica di tali proprietà sta nel fatto che è possibile trasformare un prodotto in una somma, un quoziente in una differenza e l’estrazione di una radice ennesima in una divisione per n operando solo una conversione dei numeri in questione in logaritmi, su cui è più facile operare, per poi tornare ai numeri naturali mediante una sorta di conversione inversa, detta antilogaritmo.
Le applicazioni dei logaritmi sono varie e interessano diversi campi: in statistica, vengono utilizzati per il calcolo della probabilità; in astronomia si usano nella definizione della magnitudine di una stella, che rappresenta la sua luminosità; in sismologia, la scala Richter, con la quale si misura la magnitudine di un terremoto, è una scala logaritmica e ciò comporta, nella pratica, che un terremoto di magnitudine 8 non è due volte più forte di un terremoto di magnitudine 4, ma ben 10000 volte, dove 10000 è proprio 10 elevato a 4. Ancora una volta, quindi, con i logaritmi la matematica diventa utile quotidianamente e nei settori più disparati.






